Czy komputery mogą wszystko?
16.09.2009 - Krzysztof Dryś
   Alan TuringPowyższa teoria została stworzona przez Alana Turinga przed Drugą Wojną Światową. Jej celem jest pokazanie, że komputery są w pewien sposób ograniczone. Aby dokładniej to ograniczenie zbadać, spróbujemy przyjrzeć się mu w bardziej formalny sposób.  Turing zajmował się nie tylko czysto teoretyczną informatyką. W czasie Drugiej Wojny Światowej pracował w zespole, którego zadaniem było łamanie niemieckich szyfrów. Na zdjęciu widać replikę maszyny deszyfrującej zaprojektowanej przez niego.
Turing zajmował się nie tylko czysto teoretyczną informatyką. W czasie Drugiej Wojny Światowej pracował w zespole, którego zadaniem było łamanie niemieckich szyfrów. Na zdjęciu widać replikę maszyny deszyfrującej zaprojektowanej przez niego.
Numerowanie programówWyobraźmy sobie, że ktoś ponumerował wszystkie programy napisane w c++ (albo dowolnym innym języku programowania). Jak można to zrobić? Na przykład – najpierw ustawiamy leksykograficznie (tzn. jak w słowniku) wszystkie programy, składające się z 200 znaków lub mniej. Potem ustawiamy wszystkie programy mające więcej niż 200 ale mniej niż 400 znaków. I tak dalej – w ten sposób każdy program dostanie swój numer. Jak to działa? wyobraźmy sobie, że mamy program, który ma 350 znaków i chcemy wiedzieć, jaki dostał numer. Załóżmy, że jest 1000 programów krótszych niż 200 znaków. W takim razie nasz program dostanie numer większy niż 1000. Potem patrzymy na wszystkie ciągi składające się z więcej niż 200, ale mniej niż 400 znaków zapisują poprawny program w c++. Wybieramy jest i ustawiamy leksykograficznie. W ten sposób nasz program dostanie odpowiedni numer! Ograniczymy się do programów, które czytają jedną lub dwie liczby naturalne i jako wynik zwracają również liczbę naturalną. Niech
Symbol
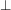 po polsku czyta się: pinezka.W informatyce służy on między innymi do oznaczania sytuacji oznaczających niepowodzenie programu. Tutaj mówimy, że program zwrócił pinezkę mając na myśli to, że się zapętlił. po polsku czyta się: pinezka.W informatyce służy on między innymi do oznaczania sytuacji oznaczających niepowodzenie programu. Tutaj mówimy, że program zwrócił pinezkę mając na myśli to, że się zapętlił.
Programy i funkcjeW ten sposób program Wiemy już, że każdemu algorytmowi odpowiada funkcja matematyczna. A czy każdej funkcji matematycznej odpowiada algorytm? Popatrzmy na funkcję:
Ciekawa funkcja obliczalnaFunkcja Funkcja
Jeżeli Ciekawa funkcja nieobliczalnaSpróbujmy teraz innej funkcji:
<
Przede wszystkim jego działanie jest niezależne od wczytanego argumentu i zawsze działa jak j-ty program na wejściu k. Stąd nazwa
Funkcja, którą oblicza program CNiech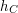 oznacza funkcję obliczaną przez program C. Spróbujmy powiedzieć o niej coś ciekawego. Pamiętajmy, że algorytm oznacza funkcję obliczaną przez program C. Spróbujmy powiedzieć o niej coś ciekawego. Pamiętajmy, że algorytm  oblicza funkcję oblicza funkcję  . Załóżmy, że . Załóżmy, że 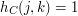 . Oznacza to, że . Oznacza to, że 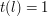 . Czyli istnieje takie . Czyli istnieje takie  , że , że 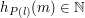 . Jeżeli jednak przypomnimy sobie to co wiemy o programie . Jeżeli jednak przypomnimy sobie to co wiemy o programie Stały(j,k) to zobaczymy, że oznacza to, że dla każdego  mamy mamy 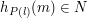 i równoważnie i równoważnie 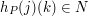 . Pokazaliśmy, że jeżeli . Pokazaliśmy, że jeżeli 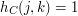 to to 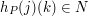 . Czyli, jeżeli dla jakiejś pary liczb . Czyli, jeżeli dla jakiejś pary liczb 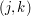 funkcja funkcja 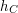 przyjmuje wartość 1, to przyjmuje wartość 1, to 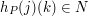 . Czyli, jeżeli dla jakiejś pary liczb . Czyli, jeżeli dla jakiejś pary liczb 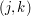 funkcja funkcja 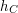 przyjmuje wartość 1, to przyjmuje wartość 1, to  -ty program nie zatrzymuje się, po wczytaniu liczby -ty program nie zatrzymuje się, po wczytaniu liczby  . .
Podobnie, jeżeli Matematyczne ograniczenia komputerówZobaczyliśmy dlaczego kompilator nie wyłapuje niektórych błędów - dlatego, że zwyczajnie nie może! Pokazaliśmy, że jest niemożliwe automatyczne sprawdzenie, czy program zapętli się dla konkretnych danych wejściowych oraz czy istnieją dane wejściowe, dla których się zapętli. Wszystkie te wyniki uzyskaliśmy szukając podobieństw i różnic między funkcjami matematycznymi i programami. W ten sposób pokazaliśmy, że to ograniczenie ma matematyczną naturę - da się go w sposób ścisły dowieść i nie da się go ominąć zatrudniając lepszego programistę, bądź kupując lepszy komputer. Wszystkie zdjęcia w artykule pochodzą z wikipedii. (5 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


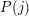 oznacza program, który dostał numer
oznacza program, który dostał numer 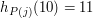 . Jeżeli natomiast
. Jeżeli natomiast 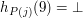 .
. 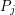 definiuje funkcję matematyczną
definiuje funkcję matematyczną 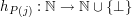 Taki zapis oznacza, że argumentami funkcji
Taki zapis oznacza, że argumentami funkcji 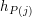 są liczby naturalne, a wartościami liczby naturalne i "zapętlanie się". Wartość funkcji
są liczby naturalne, a wartościami liczby naturalne i "zapętlanie się". Wartość funkcji  wynosi
wynosi 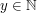 (tzn.
(tzn. 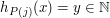 )jeżeli program
)jeżeli program  . Wartość funkcji
. Wartość funkcji 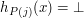 )jeżeli program
)jeżeli program 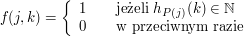
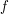 nie jest obliczalna przez żaden program. Czy jest takich funkcji więcej? Tak, a zaraz zobaczymy jeszcze jedną. Teraz dla odmiany popatrzmy na funkcję bardzo podobną do
nie jest obliczalna przez żaden program. Czy jest takich funkcji więcej? Tak, a zaraz zobaczymy jeszcze jedną. Teraz dla odmiany popatrzmy na funkcję bardzo podobną do 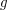 jest zdefiniowana następująco
jest zdefiniowana następująco 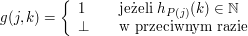
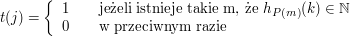
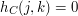 , oznacza to, że
, oznacza to, że 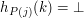 . Czyli, jeżeli
. Czyli, jeżeli 

