Liczenie po chińsku, czyli ilu jest policjantów?
13.08.2009 - Agata Murawska
  Przyjrzyjmy się bliżej pierwszej zagadce. Wiemy, że policjanci mieli być ustawiani do defilady w równych szeregach. To oznacza, że cała grupa, jeśli patrzeć na nią z góry tworzyć miała tworzyć prostokąt. Nie udawało się ustawić ich w taki sposób, gdyż zawsze ktoś zostawał.
Ponieważ nie wiemy, ile szeregów było pełnych, wprowadźmy oznaczenie, które usunie
Cóż to za dziwny symbol? Pierwsze wyrażenie czytamy: "N przystaje do 5 modulo 9". Mając trzy równania modulo dane w zagadce możemy przystąpić do szukania rozwiązania. Na razie nie bardzo widać, jak rozwiązać taki układ równań, więc zaatakujemy problem brutalnie - sprawdzając możliwe liczby, dające odpowiednie reszty. Wiemy, że policjantów było nie więcej, niż 90. Weźmy wszystkie liczby z przedziału [1, 90], które podzielone przez 9 dadzą resztę 5: Teraz usuńmy te wartości, które przy dzieleniu przez 5 dają resztę różną od 1: Wreszcie, bliscy rozwiązania, pozostawmy tylko liczby nieparzyste: Otrzymaliśmy odpowiedź – w paradzie brało udział 41 policjantów. Czy to przypadek, że rozwiązanie jest dokładnie jedno? Okazuje się, że nie. (**) Czy widzisz, czym są (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


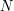 i przypomnijmy treść zadania(**):
i przypomnijmy treść zadania(**):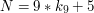
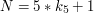
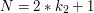
 z równań:
z równań: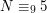
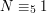
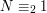
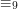 to właśnie to "modulo 9" oznaczające, jaką resztę otrzymamy dzieląc N przez 9. Równania takie, jak te powyżej, będziemy od teraz nazywać równaniami modulo (można też określać je, nieco bardziej naukowo, kongruencjami).
to właśnie to "modulo 9" oznaczające, jaką resztę otrzymamy dzieląc N przez 9. Równania takie, jak te powyżej, będziemy od teraz nazywać równaniami modulo (można też określać je, nieco bardziej naukowo, kongruencjami).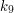 ,
, 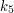 i
i 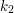 ? Mają one pewien związek z polem prostokąta.
? Mają one pewien związek z polem prostokąta.

