Błądzenie losowe
11.07.2009 - Marek Szykuła
 Czas odwiedzinWiedząc już jak wygląda spacer, możemy zastanowić się nad pytaniami:
Przyjrzyjmy się ostatniemu pytaniu. Jak można mówić o czasie skoro może być tak, że jeden szybko obejdzie wszystkie ścieżki, a drugi będzie się kręcił w kółko w nieskończoność! Istotnie może tak być, dlatego będziemy mówić zawsze o prawdopodobieństwach i średnich. Jeśli ludzik pójdzie na spacer losowy to nie możemy powiedzieć: "na pewno zdąży obejść park w 3 godziny", ale możemy powiedzieć: "z dużym prawdopodobieństwem zdąży w 3 godziny". A zatem: szansa, że ludzik chodząc bardzo długi czas nie obejdzie całego parku jest bardzo mała. Musiałby przecież za każdym razem unikać wyboru jakiejś drogi, więc im dłużej spaceruje tym mniejsza szansa, że coś zostało. Ale nigdy nie mamy gwarancji, że po określonym czasie spacerowania uda się obejść cały park. Możemy także powiedzieć więcej: obejście wszystkiego zajmuje średnio dany czas. Każdy konkretny park ma jakiś swój własny średni czas odwiedzin. Da się go zmierzyć w prosty sposób: wysyłając na taki spacer dużo ludzików, mierząc ich czas obejścia i licząc średnią arytmetyczną. Taki średni czas obejścia całego parku nazywamy czasem pokrycia. Zobaczmy przykład spaceru losowego na prostej drodze: Tym razem ludzik może zawrócić w każdym miejscu na drodze. Jak widać bardzo utrudnia mu to dojście dokądkolwiek. Przyjmiemy tutaj, że w jednej jednostce czasu ludzik idzie w jednym kierunku, po czym może zawrócić. Ile czasu zajmie mu przejście całej drogi z jednego końca do drugiego? Odpowiedź może dać taki eksperyment: stawiamy ludzika na jednym końcu i mierzymy jak szybko dojdzie na drugi. Wyniki dla różnych odległości są następujące:
Można zauważyć, że ten średni czas wynosi Od czego zależy jaki jest czas pokrycia? Oczywiście od układu dróg, ale nie tylko. Może on też istotnie zależeć także od miejsca jego rozpoczęcia. (8 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


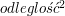 . Tak też istotnie jest, dla każdej odległości średni czas przejścia wynosi właśnie tyle.
. Tak też istotnie jest, dla każdej odległości średni czas przejścia wynosi właśnie tyle.

