Gra sterowana kamerą - bieg po farbę
02.07.2017 - Filip Mróz
  Nie wylewaj Pan farby!Zaprogramujmy ostatnią "atrakcję" etapu biegu czyli wylewanie się farby.
Gotowy kod z tej części można znaleźć w paczce ze źródłami w katalogu: Wersja_5_Wylewanie_farby
Element ten sprawi, że gracz, poza biegiem, będzie musiał się koncentrować na trzymaniu wiadra w pozycji poziomej. W przeciwnym wypadku może przynieść do płotu prawie puste wiadro. Może nawet uznać, że bardziej opłaca mu się wylać resztę farby i wrócić po nowe, pełne wiadro. Nasuwają się pytania: O co chodzi? Jakie wiadro? Jak sprawdzić czy jest przechylone? Wiadro w naszej grze będzie reprezentowane przez podłużny przedmiot i właśnie zależnie od kąta jego nachylenia, farba będzie znikać albo spokojnie czekać na czas malowania. Do wykrycia wiadra wykorzystamy metody utworzone w poprzednim artykule. Alternatywą byłoby użycie dwóch przedmiotów i wyznaczenie kąta nachylenia wiadra z kąta nachylenia linii łączącej ich środki. Byłoby to jednak dość nienaturalne i bardziej podatne na błędy (pewniej jest wykryć jeden duży obiekt niż dwa małe). Dlatego zaimplementujemy pierwsze rozwiązanie.
Całość wykonamy podobnie jak w przypadku Wylewanie farby i wyświetlanie wiadra
Zaczniemy implementację od dodania funkcji class StanBiegu { ( double StanBiegu::wyznaczSzybkoscUtratyFarby(Mat obraz) { return 0; }
Niech w else { polozenie -= czas * predkosc; niesionaFarba -= czas * wyznaczSzybkoscUtratyFarby(obraz); niesionaFarba = max(niesionaFarba,0.0); }
Prędkość wypływu farby będzie zależeć tylko od przechylenia wiadra, którego wyznaczenie zrzucimy na 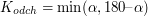
Gracz powinien mieć szansę doniesienia pełnego wiadra, więc będziemy go karać dopiero wtedy, gdy kąt odchylenia przekroczy double StanBiegu::wyznaczSzybkoscUtratyFarby(Mat obraz) { nachylenieWiadra = przetwarzanieObrazow.wyznaczNachylenie(obraz); double katOdPoziomu = min(nachylenieWiadra,180-nachylenieWiadra); if(katOdPoziomu < 10) return 0; else return POJEMNOSC_WIADRA * katOdPoziomu / 90; }
Aby umożliwić kompilację tego kodu, dodajmy deklarację oraz pseudo implementację: double wyznaczNachylenie(Mat obraz); double PrzetwarzanieObrazowBiegu::wyznaczNachylenie(Mat obraz) { return 90; }
Część odpowiedzialna za wylewanie farby jest gotowa, ale gracz będzie mógł to zauważyć tylko po malejącym pasku posiadanej farby. Aby to zmienić, dodamy w void rysujObroconyProstokat(Mat gdzie, RotatedRect &prostokat, Vec3b kolor);
Do implementacji wykorzystamy strukturę void Uzytki::rysujObroconyProstokat(Mat gdzie, RotatedRect &prostokat, Vec3b kolor) { Point2f tmprogi[4]; Point rogi[4]; // Musimy przerobić współrzędne punktów na całkowite. prostokat.points(tmprogi); for(int i=0;i<4;i++) rogi[i] = (Point)tmprogi[i]; fillConvexPoly(gdzie,rogi,4,(Scalar)kolor); }
Z takim narzędziem przejdźmy do metody wyświetlającej // Tylko jeśli wracamy z farbą. if(niesionaFarba != 0) { Point srodek = Point(gdzie.cols/2, gdzie.rows/2); RotatedRect obrocony = RotatedRect(srodek,Size(150,70),nachylenieWiadra); RotatedRect obroconyPasek = RotatedRect(srodek,Size(150,30),nachylenieWiadra); // Rysuj szare wiadro. Uzytki::rysujObroconyProstokat(gdzie, obrocony, Vec3b(100,100,100)); // Rysuj kolorowy pasek pośrodku wiadra. Uzytki::rysujObroconyProstokat(gdzie, obroconyPasek, kolorFarby); } } Utworzone w ten sposób wiadro podczas rozgrywki będzie wyglądało tak:  Kalibracja wiadra
Podobnie jak w przypadku wykrywania pędzla (patrz Gra sterowana kamerą - pomaluj płot), aby wykryć wiadro w obrazie, trzeba wcześniej wyznaczyć jego parametry (m.in. barwę). Ponieważ
Dodajmy zmodyfikowaną kopię metody void kalibrujWiadroGracza(StanGracza &gracz) { kamera >> aktualnyObraz; flip(aktualnyObraz,aktualnyObraz,1); aktualnyObraz.copyTo(wyswietlanyObraz); // Wypisz informację dla gracza. Uzytki::wypiszTekst(wyswietlanyObraz, gracz.nazwa + "! Wybierz wiadro!",Point(0,25)); wyswietlZachowujacProporcje(wyswietlanyObraz); waitKey(3000); while(waitKey(100)!='k') { kamera >> aktualnyObraz; flip(aktualnyObraz,aktualnyObraz,1); aktualnyObraz.copyTo(wyswietlanyObraz); // Niech okno będzie prostokątne. Rect polozenieOkna = Rect(aktualnyObraz.cols/2-ROZMIAR_OKNA_KALIBRACJI_WIADRA/2,aktualnyObraz.rows/2-40,ROZMIAR_OKNA_KALIBRACJI_WIADRA,40); Mat okno = Mat(aktualnyObraz,polozenieOkna); // Ustaw parametry wiadra na podstawie zawartości okna. gracz.ustawParametryWiadra(okno); Mat pikseleWiadra = gracz.stanBiegu.przetwarzanieObrazow.wybierzPiksele(aktualnyObraz); wyswietlanyObraz.setTo(Scalar(255,0,0),pikseleWiadra); rectangle(wyswietlanyObraz,polozenieOkna,Scalar(0,255,0),3); wyswietlZachowujacProporcje(wyswietlanyObraz); int liczbaPikseliWiadraOkno = countNonZero(Mat(pikseleWiadra,polozenieOkna)); int liczbaPikseliWiadra = countNonZero(pikseleWiadra); if(2*liczbaPikseliWiadraOkno > liczbaPikseliWiadra) { break; } } } Ze względu na podobieństwo obu metod można się pokusić o odpowiednią refaktoryzację. Niech to będzie zadanie dla ambitnych czytelników. Musimy jeszcze dodać stałą oznaczającą długość dłuższego boku okna kalibracji wiadra: const int ROZMIAR_OKNA_KALIBRACJI = 50; const int ROZMIAR_OKNA_KALIBRACJI_WIADRA = 150; Następnie dodajmy metodę wyznaczającą i ustawiającą dobre parametry wiadra na podstawie podanego obrazu: void ustawParametryWiadra(Mat wiadro); void StanGracza::ustawParametryWiadra(Mat wiadro) { Vec3b kolor; int wartoscGraniczna; PrzetwarzanieObrazow::wyliczDobreParametry(wiadro,kolor,wartoscGraniczna); stanBiegu.przetwarzanieObrazow.kolor = kolor; stanBiegu.przetwarzanieObrazow.wartoscGraniczna = wartoscGraniczna; } Na koniec użyjmy naszej metody kalibrującej przed rozpoczęciem rozgrywki, a zaraz po kalibracji pędzla: kalibrujPedzelGracza(stanGry.gracze[0]); kalibrujWiadroGracza(stanGry.gracze[0]); if(liczbaGraczy==2) { kalibrujPedzelGracza(stanGry.gracze[1]); kalibrujWiadroGracza(stanGry.gracze[1]); } Wyznaczanie przechylenia wiadraPozostała nam ostatnia, a zarazem najciekawsza część pracy, czyli implementacja metod znajdujących wiadro oraz kąt jego nachylenia. Algorytm tradycyjnie już będzie składał się z trzech etapów:  Zauważmy, że pierwsze dwa etapy mamy już zrealizowane, ponieważ takie same etapy (oczywiście z innymi parametrami) są już wykonywane podczas szukania pędzla. Dodajmy deklarację ostatniego etapu: double wyznaczNachylenieKonturu(Kontur wybranyKontur); double PrzetwarzanieObrazowBiegu::wyznaczNachylenie(Mat obraz) { Mat piksele = wybierzPiksele(obraz); Kontur wybranyKontur = filtruj(piksele); return wyznaczNachylenieKonturu(wybranyKontur); } Do napisania pozostaje nam tylko wyznaczenie nachylenia obiektu opisanego przez kontur. Zastanówmy się, jak można zdefiniować takie nachylenie. Załóżmy, że nasz przedmiot wygląda tak: 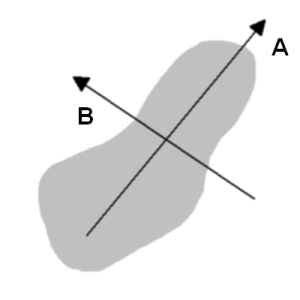
Która oś lepiej oddaje ukierunkowanie przedmiotu? Oczywiście jest to oś A. Po czym można to poznać? Wyobraźmy sobie, że mamy płaski przedmiot o kształcie pokazanym powyżej. Wokół której osi łatwiej nam będzie go obracać? Właśnie wokół osi A, ponieważ masa jest bardziej skupiona wokół niej. W fizyce tę własność nazywa się momentem bezwładności (oznaczanym jako 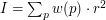 gdzie gdzie  to odległość piksela od osi, a to odległość piksela od osi, a 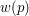 to wartość piksela to wartość piksela
Mamy więc metodę pozwalającą wybrać z paru potencjalnych osi tę najlepszą (o najmniejszym 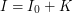 , gdzie , gdzie 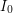 to oś równoległa do osi to oś równoległa do osi 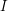 , ale przechodząca przez środek masy, , ale przechodząca przez środek masy, 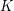 – pewna nieujemna liczba – pewna nieujemna liczba
Można więc wywnioskować, że oś obrotu o najmniejszym Pozostaje pytanie, czy można dokładnie (analitycznie) wyznaczyć tę najlepszą oś? Okazuje się, że tak. Do rozwiązania potrzeba trochę trygonometrii oraz umiejętności wykorzystywania pochodnych do znajdowania ekstremów funkcji. Zainteresowanych odsyłam do całkiem ładnego wyprowadzenia dla przypadku ciągłego. Ostateczne rozwiązanie okazuje się wykorzystywać momenty, które poznaliśmy już w poprzednim artykule: 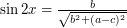
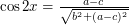 gdzie
gdzie  - - 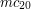 , ,  – – 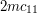 , ,  – – 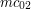
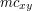 oznaczają momenty centralne, czyli liczone w układzie, którego środek pokrywa się ze środkiem masy obiektu. oznaczają momenty centralne, czyli liczone w układzie, którego środek pokrywa się ze środkiem masy obiektu.
Załóżmy, że mamy już 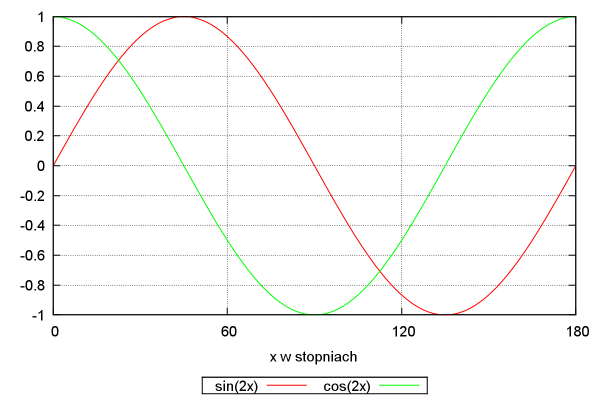 Gdy wyliczymy arccosinusa z pewnej wartości cosinusa, to otrzymamy jeden z dwóch kątów (jak przedstawiono na wykresie): 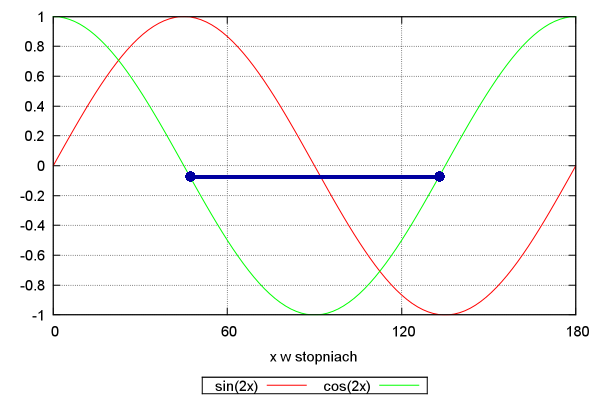
Skąd wiadomo, który z nich jest właściwy? Zauważmy, że możemy wykorzystać do tego wartość sinusa. Jeśli sinus jest dodatni, to wybierzemy Udało nam się uporać z trygonometrią, więc można się zabrać za implementację pomysłu. Zaczniemy od sprawdzenia, czy wcześniejszym krokom udało się wykryć wiadro: double PrzetwarzanieObrazowBiegu::wyznaczNachylenieKonturu(Kontur kontur) { if(kontur.size()==0 || abs(contourArea(kontur)) < MINIMALNY_ROZMIAR_KONTURU){ return 90; } Jeśli się nie udało to uznajemy, że nachylenie jest maksymalne, gdyż gracz mógł ukryć gdzieś wiadro próbując uniknąć całej zabawy z utratą farby. Gdy mamy odpowiednio duży kontur wiadra, to wyliczamy dla niego momenty oraz momenty centralne. Udowodnienie wzorów wyliczających momenty centralne na podstawie zwykłych momentów i położenia środka masy zostawiam jako zadanie: else { Moments momenty = moments(kontur); Point2f srodekMasy(momenty.m10/momenty.m00,momenty.m01/momenty.m00); // Wyliczmy wartość momentów centralnych. double c11 = momenty.m11 - srodekMasy.x * momenty.m01; double c20 = momenty.m20 - srodekMasy.x * momenty.m10; double c02 = momenty.m02 - srodekMasy.y * momenty.m01; Następnie, zgodnie ze wcześniejszymi ustaleniami, wyliczamy wartości sinusa i cosinusa, a następnie kąt nachylenia wynikający tylko z wartości cosinusa: double sinus = 2*c11/sqrt(4*c11*c11 + (c20-c02)*(c20-c02)); double cosinus = (c20-c02)/sqrt(4*c11*c11 + (c20-c02)*(c20-c02)); // Otrzymamy kąt w radianach, które musimy przeliczyć na stopnie. double phi = acos(cosinus)/2*360/2/3.14; Na koniec sprawdzamy wartość sinusa, by ustalić właściwy kąt: if(sinus > 0) return abs(phi); else return 180 - abs(phi); } } W zasadzie to już wszystko, ale sprawdźmy na koniec, czy wykrywanie nachylenia wiadra działa jak należy: 
 Mechanizm wydaje się działać bez zarzutu i jest dość dokładny. Potencjalnie można wykorzystać tak wyliczone nachylenie do sterowania motorem czy samochodem w jakiejś grze. Na pewno będzie to dużo wygodniejsze niż używanie do tego celu klawiatury. Prace nad grą można uznać za zakończone. Gratulacje! W ramach nagrody możesz oddać się rozrywce! |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


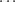
![$ \alpha \in [0,180] $](/files/tex/08a0947ab7ed924fae759274d8ca66a1580b6c5f.png) liczony od lewej strony zgodnie z ruchem wskazówek zegara. Kąt odchylenia wiadra od poziomu będzie wtedy wynosił:
liczony od lewej strony zgodnie z ruchem wskazówek zegara. Kąt odchylenia wiadra od poziomu będzie wtedy wynosił:
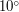 . Dodatkowo, przy maksymalnym kącie (prostym), pełne wiadro opróżni się w sekundę. Powstała funkcja prezentuje się następująco:
. Dodatkowo, przy maksymalnym kącie (prostym), pełne wiadro opróżni się w sekundę. Powstała funkcja prezentuje się następująco:
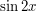 i
i 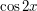 . Jak teraz, na ich podstawie, wyznaczyć kąt
. Jak teraz, na ich podstawie, wyznaczyć kąt  ? Funkcja
? Funkcja 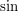 jest różnowartościowa tylko w przedziale 180 stopni, natomiast gdy kąt to
jest różnowartościowa tylko w przedziale 180 stopni, natomiast gdy kąt to 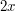 , przedział maleje do 90 stopni. Chcemy wyznaczyć nachylenie w przedziale od 0 do 180 stopni, dlatego sam sinus nie wystarczy i będziemy musieli wykorzystać też wartość cosinusa. Przyjrzyjmy się wykresom obu funkcji:
, przedział maleje do 90 stopni. Chcemy wyznaczyć nachylenie w przedziale od 0 do 180 stopni, dlatego sam sinus nie wystarczy i będziemy musieli wykorzystać też wartość cosinusa. Przyjrzyjmy się wykresom obu funkcji:
![$ x \in [0^{\circ} , 90^{\circ}] $](/files/tex/16f3e69f886d89d1e53a52159975f55400923692.png) stopni, w przeciwnym wypadku weźmiemy
stopni, w przeciwnym wypadku weźmiemy ![$ x \in [90^{\circ}, 180^{\circ}] $](/files/tex/5419a67ee9f55014c50473ec5638c82421898fb9.png) , który, jak łatwo zauważyć, ma wartość 180 – x.
, który, jak łatwo zauważyć, ma wartość 180 – x.


