Sieci neuronowe: czego można się nauczyć bez nauczyciela?
22.09.2012 - Patryk Filipiak
   Sieci KohonenaW latach 80. XX wieku Teuvo Kohonen opracował model jednej z najczęściej stosowanych obecnie sieci neuronowych, znany jako SOM (z ang. Self-organizing Maps, czyli samoorganizujące się mapy). Swój sukces zawdzięczają one temu, że pozwalają stworzyć mapy przestrzeni bardzo wysokich wymiarów, a uczenie takich sieci nie wymaga nadzoru. Innymi słowy, przeprowadzają one klasteryzację takich przestrzeni, budując jednocześnie ich dwuwymiarowy obraz. Architektura SOMArchitektura SOM jest niezwykle prosta. Najwygodniej jest zilustrować ją graficznie w postaci siatki. 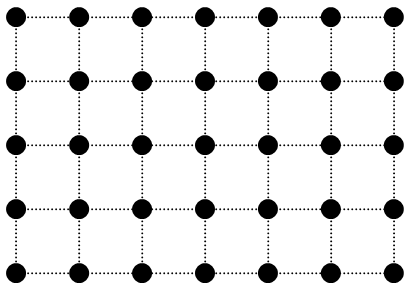
Każda czarna kropka w takiej siatce reprezentuje jeden neuron (komórkę nerwową). Główną rolą neuronów jest reagowanie na bodźce. Co najważniejsze, każdy z nich jest przystosowany do tego, by reagować wyłącznie na bodźce z bardzo wąskiego zakresu. Na przykład, gdybyśmy mieli do czynienia z siecią reagującą na barwy, neuron odpowiedzialny za reakcję na barwę czerwoną reagowałby bardzo mocno na intensywną czerwień, nieco słabiej na kolor wiśniowy, za to na kolor pomarańczowy, brązowy czy czarny nie reagowałby wcale. Tam, gdzie „milczałby” neuron czerwieni, zareagowaliby jego sąsiedzi. Dzięki temu sieć jako całość może być wrażliwa na całe spektrum barw. W tym miejscu kluczową rolę odgrywa mapa. Każdy neuron jest połączony z neuronami leżącymi w jego bezpośrednim otoczeniu. Takie otoczenie nie jest przypadkowe. Kontynuując przykład sieci rozpoznającej barwy, neurony uwrażliwione na kolor pomarańczowy albo brązowy leżałyby w bliskim sąsiedztwie neuronu odpowiedzialnego za reagowanie na barwę czerwoną. Z kolei neuronów reagujących na barwę niebieską bądź zieloną, należałoby się spodziewać znacznie dalej. W ten sposób prosta siatka neuronów staje się mapą badanej przestrzeni (w tym przypadku: przestrzeni barw). Zwróćmy uwagę, że taka siatka pełni rolę bardzo uniwersalnej mapy. Nic nie stoi na przeszkodzie, żeby zorganizowane w taki sposób neurony reagowały nie tylko na barwy, ale także na wspomniane wcześniej temperatury powietrza itp. Pewien neuron mógłby być wrażliwy na temperatury rzędu 15-18oC o poranku, inny zaś za temperatury z przedziału 28-30oC w południe. Tak skonstruowana sieć zapewniłaby nam jednocześnie pewną klasteryzację badanej przestrzeni. W jaki sposób? Przeanalizujemy to na przykładzie. W najprostszym przypadku, opisywaliśmy pomiary temperatury powietrza w ciągu dnia przy pomocy czterech liczb reprezentujących wskazania termometru o ustalonych godzinach 6:00, 12:00, 18:00 i 00:00. Mówiliśmy też, że nie da się takich zestawów pomiarów przedstawić wprost na wykresie. Nie jesteśmy więc w stanie dokładnie narysować podziału przestrzeni na klastry, ponieważ byłyby to zbiory 4-wymiarowe. To, co możemy zrobić, to zbudować mapę takich klastrów. Pomoże nam w tym architektura SOM. Skoro klasteryzacja polega na podzieleniu przestrzeni na obszary, w których występują podobne przypadki, zamiast grupować w klastry przypadki, możemy grupować neurony, które na nie reagują. Nie zobaczymy w ten sposób dokładnie badanej przestrzeni, ale zobaczymy jej mapę. Przykładową mapę przestrzeni pomiarów temperatury powietrza przedstawia poniższy rysunek. 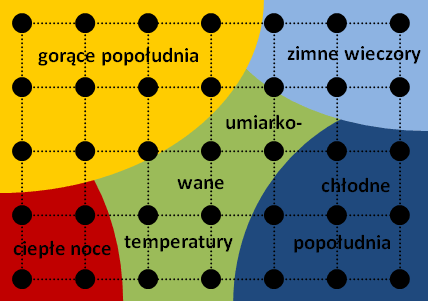
Zauważmy, że pewne obszary nachodzą na siebie. Nic przecież nie stoi na przeszkodzie, żeby w dni, w których popołudnia były gorące, występowały również zimne wieczory albo wprost przeciwnie - ciepłe noce. Warto też odnotować, że gorące i chłodne popołudnia znalazły się na obszarach przeciwległych. Sytuacja z zimnymi wieczorami i ciepłymi nocami jest podobna. Obszar umiarkowanych temperatur znalazł się zaś mniej więcej w środku. Uczenie SOMSOM, jak każda sieć neuronowa, wymaga wytrenowania (lub inaczej nauczenia). Do nauki bez nadzoru, jak wspomnieliśmy, nie jest potrzebny nauczyciel, jednak - z całą pewnością - potrzebny jest czas. Tak więc chcemy nauczyć SOM naszych pomiarów temperatury powietrza. Co to właściwie znaczy? Jak duża powinna być sieć? Jakich efektów oczekujemy i kiedy będziemy mogli uznać, że sieć jest już nauczona? Załóżmy, że dysponujemy pomiarami temperatury wykonywanymi codziennie przez całe lato. Uczenie polega na tym, żeby wszystkie te pomiary zaprezentować sieci. Zadaniem sieci natomiast jest znalezienie wyników podobnych do siebie, pogrupowanie ich w klastry i zbudowanie mapy uzyskanego podziału. Po przejściu przez tak rozumiany proces uczenia, sieć powinna z dużą skutecznością poprawnie klasyfikować kolejne pomiary, tzn. przypisywać je do odpowiednich klastrów. Dla przykładu, jeśli wytrenowanej sieci zaprezentujemy pomiary z lipcowego dnia, w którym temperatura o godzinie osiemnastej wynosiła zaledwie 8oC, to oczekujemy, że pomiar ten sklasyfikowany zostanie raczej w grupie zimnych wieczorów bądź chłodnych popołudni aniżeli ciepłych nocy. Algorytm, który realizuje nasza sieć w celu wytrenowania, nie jest skomplikowany. Na samym początku przyjmujemy, że sieć nie wie nic. Pojawia się pytanie, co to znaczy nie wiedzieć nic na gruncie neuronów. Najprostszą, a zarazem skuteczną i powszechnie stosowaną metodą jest losowy dobór bodźców, na które mają reagować poszczególne neurony. Skoro nasza sieć ma reagować jednocześnie na cztery pomiary temperatury w ciągu doby, to zaczynamy od wylosowania po jednym zestawie czterech liczb dla każdego z neuronów. Powinny to być oczywiście liczby losowe z "rozsądnego" przedziału. Zważywszy, że pomiarów dokonujemy latem, nie spodziewamy się raczej ujemnych temperatur, podobnie jak nie przypuszczamy, by temperatura wzrosła w Polsce powyżej 40 stopni Celsjusza. Zresztą, nawet jeśli się tak zdarzy, będzie to przypadek odosobniony, więc pozbawiony wpływu na ogólną sytuację. Gdy uda nam się utworzyć kompletnie chaotyczną sieć neuronów reagujących na zupełnie losowe bodźce, musimy powziąć kroki mające na celu zgromadzenie wiedzy, którą będziemy prezentować sieci. Weźmy pierwszy pomiar. Niech to będzie na przykład (14.9, 21.3, 20.8, 15.6). Oznaczmy go jako A. Bez względu na to, jak odległy jest taki pomiar A od bodźców, na które uwrażliwione są losowo skonfigurowane neurony, zawsze znajdzie się taki neuron, który będzie mu najbliższy. Niech to będzie na przykład neuron, który najmocniej reaguje na wartości (16.5, 23.7, 22.1, 16.8). Oznaczmy go jako B. To właśnie ten neuron zostanie wytypowany do nauczenia się przedstawionego przykładu. Proces nauki osiągniemy poprzez przesunięcie konfiguracji neuronu z punktu B, na który dotychczas był on wrażliwy, w stronę punktu A, który został mu zaprezentowany. Postępujemy tak kolejno dla wszystkich posiadanych pomiarów: bierzemy pomiar, znajdujemy neuron, który najsilniej na niego reaguje i modyfikujemy ten neuron tak, aby reagował na dany pomiar jeszcze silniej. W praktyce możliwa jest sytuacja, gdy dwa neurony okażą się wrażliwe na bodźce, które są równoodległe od zaprezentowanego przykładu. Wtedy możemy wybrać losowo jednego spośród nich. Należy się zastanowić, czy każdorazowe wybieranie tylko jednego (najbliższego) neuronu jest najlepszym rozwiązaniem. Badania pokazują, że warto (zwłaszcza w początkowej fazie uczenia, gdy sieć jest jeszcze mocno chaotyczna) modyfikować nie tylko jeden neuron, ale również całą grupę jego sąsiadów (tak, jak pokazuje to rysunek). 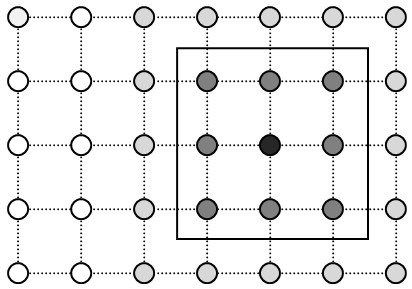
|
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




